前言

优化器是用来更新参数的，其以梯度，lr，参数parameters以及其他值例如动量作为输入，经过一系列变换，得到新的参数。

而发展到如今，有很多的优化器，他们的不同之处就是这个变换的不同。

我们仔细想象，变换的不同，其实也可以认为是侧重点不同，不同的优化器有各自的特点和用武之地，他们考虑的因素有如下：

1. 学习率能否动态变化。如果是固定的，那么选小了，收敛太慢；选大了，阻碍收敛甚至容易发散。如果是变化的，该如何变化。（注：pytorch中的Learning rate schedule的方式，随着epoch数去减小学习率（lr退火），也只能用一个事先定义好方式去annealing，不能根据当前batch数据的特点去动态的decay。不能算是真正的学习率动态变化）
2. 所有的参数都用的是一个学习率，不能自适应地调节。
3. 如何加速收敛，逃离极小值点。

本文参考了以下文章，所以相当于是读书笔记：
1.https://zhuanlan.zhihu.com/p/77503211

GD

1.批梯度下降 BGD (Batch gradient descent)

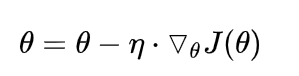
2.随机梯度下降 SGD (Stochastic gradient descent)

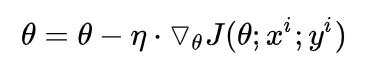
3.小批梯度下降 MBGD (Mini-batch gradient descent)

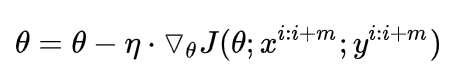
1，2，3分别是所有样本，单个样本，部分样本带入模型，得到损失，计算梯度，更新参数。

显然，我们通常用的都是3，其已经是标配了。比如Pytorch中的DataLoader里设置batch_size。

1的缺点在于需要将数据全部放在内存。2的缺点在于参数更新抖动比较大，因为前后两个样本可能有一定差距，前面往左更新，后面又往右边更新，不好。而方法3，取部分可以某种程度上代表整体，求平均的损失，求梯度，更新参数，更加稳定。

注：我们今后所讲的SGD都是指代上面的3，而不是2。这个S你可以理解为随机抽取部分样本代替总体样本分布的意思。

momentum

momentum是动量的意思，其意思是说保持上次参数更新的方向一定程度地不变。其优点是：

1. 大部分时候可以加速收敛，有点像下坡，带着惯性下得很快。
2. 正是因为有可能冲得太猛，其更有可能冲出极小值点。

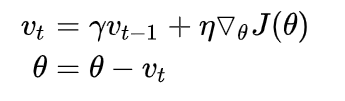
我们让$v_0=0$即可一直迭代下去。其中前面那个希腊字母是momentum参数，后面那个是lr参数。

Nesterov accelerated gradient (NAG)

Nesterov是一个人。

可以看到，上面的momentum可以分为两个步骤，先$\theta ?\gamma v_{t?1}$，成为${\theta }^{{}^{\prime }}$，然后再减去关于之前的$\theta$的梯度。

现在Nesterov换一种方法，其第二步换成减去关于现在${\theta }^{{}^{\prime }}$的梯度。

pytorch中SGD的momentum和Nesterov

使用方法

pytorch中的集成了momentum和Nesterov的SGD实现方式如下，和之前讲的略有不同，但功能差不多。

下面是实现了momentum的SGD。

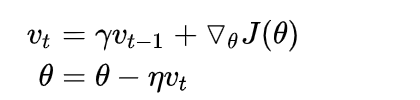
相当于两个超参数的乘积才是momentum这个超参数了，其他一样。所以lr参数变得更加重要，因为其会直接影响两个嘛。

下面是实现了Nestero的SGD。



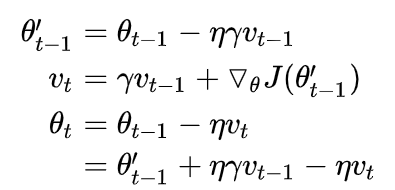
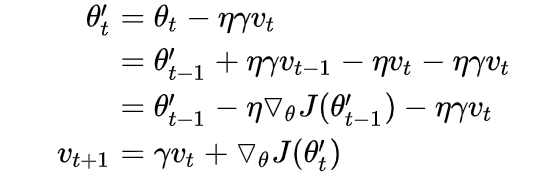
上面很容易，所有步骤都写齐了，仔细看看就可以。

weight_decay

是L2正则，目的是防止过拟合。例如下图就过拟合了。

我们发现：过拟合有一个特点：那就是导数很大。

所以我们的想法就是：不让其导数很大，从而希望减轻过拟合。那怎么让其导数不要很大呢？你看上面那个函数，大概是这样的：$a{x}^5+b{x}^4+c{x}^3+dx$，其中$a,b,c,d$是我们要学的参数。其导数为：$5a{x}^4+4b{x}^3+3c{x}^2+d$，我们希望导数不要很大，那么当然可以让$a,b,c,d$小一些喽，因为参数是我们可以控制的，$x$是输入，我们无法控制。$a,b,c,d$更小，从而我们可以在损失函数上加上一项$los{s}_w=\frac{1}{4}?\frac{1}{2}(a^2+b^2+c^2+d^2)$，这个东西就叫做L2正则项（平方）。前面的那个1/4是4个参数取平均，后面那个1/2是为了这一项loss对参数$a$等求偏导之后系数为1。

那么我们得到了完整的loss，$loss=los{s}_x+los{s}_w$，在实际中，我们会对这两项做一个平衡，即：
$loss=los{s}_x+\lambda los{s}_w$

其中$\lambda$ 就称为权重衰减系数。显然，这个数越大，那么优化之后，权重就会越小，否则损失太大。